An ant on the move
February 22, 2014
On the Euclidean plane, an ant travels from point A(0, 1) to point B(d, 1) for an integer d.
In each step, the ant at point (x0, y0) chooses one of the lattice points (x1, y1) which satisfy x1 ≥ 0 and y1 ≥ 1 and goes straight to (x1, y1) at a constant velocity v. The value of v depends on y0 and y1 as follows:
- If y0 = y1, the value of v equals y0.
- If y0 ≠ y1, the value of v equals (y1 - y0) / (ln(y1) - ln(y0)).
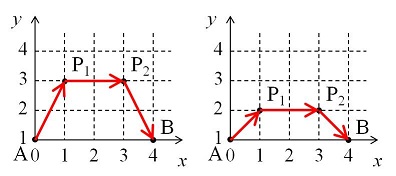
The left image is one of the possible paths for d = 4. First the ant goes from A(0, 1) to P1(1, 3) at velocity (3 - 1) / (ln(3) - ln(1)) ≈ 1.8205. Then the required time is sqrt(5) / 1.8205 ≈ 1.2283. From P1(1, 3) to P2(3, 3) the ant travels at velocity 3 so the required time is 2 / 3 ≈ 0.6667. From P2(3, 3) to B(4, 1) the ant travels at velocity (1 - 3) / (ln(1) - ln(3)) ≈ 1.8205 so the required time is sqrt(5) / 1.8205 ≈ 1.2283. Thus the total required time is 1.2283 + 0.6667 + 1.2283 = 3.1233.
The right image is another path. The total required time is calculated as 0.98026 + 1 + 0.98026 = 2.96052. It can be shown that this is the quickest path for d = 4.
Let F(d) be the total required time if the ant chooses the quickest path. For example, F(4) ≈ 2.960516287. We can verify that F(10) ≈ 4.668187834 and F(100) ≈ 9.217221972.
Find F(10000). Give your answer rounded to nine decimal places.
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter