Crisscross Ellipses

E_a is an ellipse with an equation of the form x² + 4y² = 4a². E_a' is the rotated image of E_a by θ degrees counterclockwise around the origin O(0, 0) for 0° < θ < 90°.

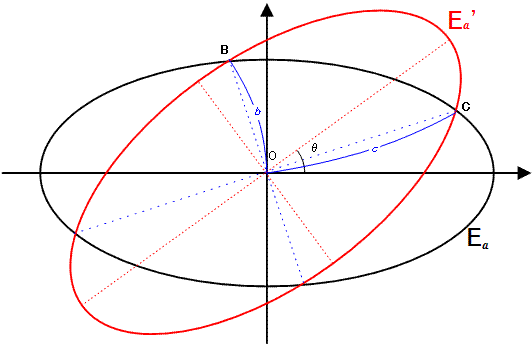
b is the distance to the origin of the two intersection points closest to the origin and c is the distance of the two other intersection points. We call an ordered triplet (a, b, c) a canonical ellipsoidal triplet if a, b and c are positive integers. For example, (209, 247, 286) is a canonical ellipsoidal triplet.

Let C(N) be the number of distinct canonical ellipsoidal triplets (a, b, c) for a ≤ N. It can be verified that C(10³) = 7, C(10⁴) = 106 and C(10⁶) = 11845.

Find C(10¹⁷).

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter