Cross-hatched triangles
October 13, 2007
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
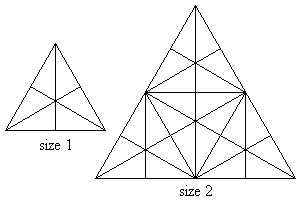
Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n2 size 1 triangle building blocks.
If we denote T(n) as the number of triangles present in a triangle of size n, then
T(1) = 16 T(2) = 104
Find T(36).
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter