Cyclic paths on Sierpiński graphs

- A Sierpiński graph of order-1 (S₁) is an equilateral triangle. - S_n+1 is obtained from S_n by positioning three copies of S_n so that every pair of copies has one common corner.

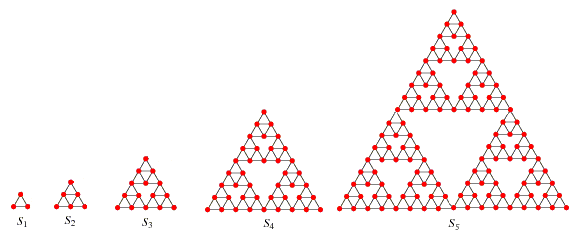
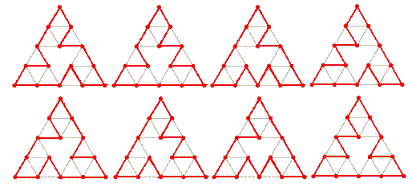
Let C(n) be the number of cycles that pass exactly once through all the vertices of S_n. For example, C(3) = 8 because eight such cycles can be drawn on S₃, as shown below:

It can also be verified that : C(1) = C(2) = 1 C(5) = 71328803586048 C(10 000) mod 10⁸ = 37652224 C(10 000) mod 13⁸ = 617720485

Find C(C(C(10 000))) mod 13⁸.

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter