Gnomon numbering

For integers m, n (0 ≤ n < m), let L(m, n) be an m×m grid with the top-right n×n grid removed.

For example, L(5, 3) looks like this:

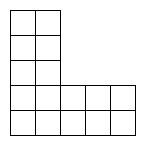
We want to number each cell of L(m, n) with consecutive integers 1, 2, 3, ... such that the number in every cell is smaller than the number below it and to the left of it.

For example, here are two valid numberings of L(5, 3):

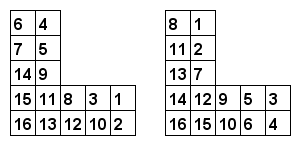
Let LC(m, n) be the number of valid numberings of L(m, n). It can be verified that LC(3, 0) = 42, LC(5, 3) = 250250, LC(6, 3) = 406029023400 and LC(10, 5) mod 76543217 = 61251715.

Find LC(10000, 5000) mod 76543217.

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter