Minkowski Sums
January 17, 2009
Let Sn be the regular n-sided polygon – or shape – whose vertices
vk (k = 1,2,…,n) have coordinates:
| xk = cos( 2k-1/n ×180° ) | |
| yk = sin( 2k-1/n ×180° ) |
Each Sn is to be interpreted as a filled shape consisting of all points on the perimeter and in the interior.
The Minkowski sum, S+T, of two shapes S and T is the result of
adding every point in S to every point in T, where point addition is performed coordinate-wise:
(u, v) + (x, y) = (u+x, v+y).
For example, the sum of S3 and S4 is the six-sided shape shown in pink below:
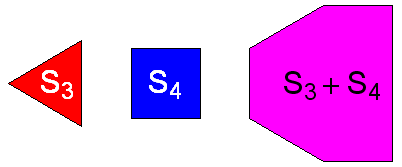
How many sides does S1864 + S1865 + … + S1909 have?
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter