Pizza Toppings
March 05, 2010
You are given a pizza (perfect circle) that has been cut into m·n equal pieces and you want to have exactly one topping on each slice.
Let f(m,n) denote the number of ways you can have toppings on the pizza with m different toppings (m ≥ 2), using each topping on exactly n slices (n ≥ 1). Reflections are considered distinct, rotations are not.
Thus, for instance, f(2,1) = 1, f(2,2) = f(3,1) = 2 and f(3,2) = 16. f(3,2) is shown below:
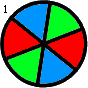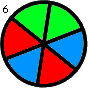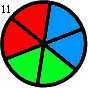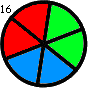
Find the sum of all f(m,n) such that f(m,n) ≤ 1015.
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter