Sequence of points on a hyperbola
April 07, 2013
Let H be the hyperbola defined by the equation 12x2 + 7xy - 12y2 = 625.
Next, define X as the point (7, 1). It can be seen that X is in H.
Now we define a sequence of points in H, {Pi : i ≥ 1}, as:
- P1 = (13, 61/4).
- P2 = (-43/6, -4).
- For i > 2, Pi is the unique point in H that is different from Pi-1 and such that line PiPi-1 is parallel to line Pi-2X. It can be shown that Pi is well-defined, and that its coordinates are always rational.
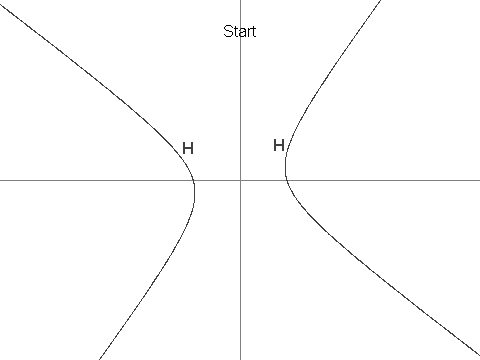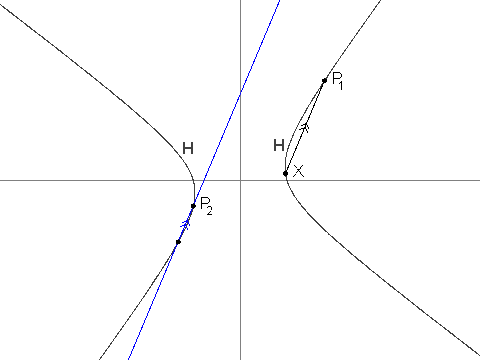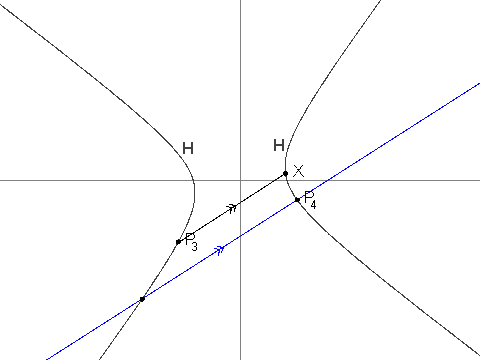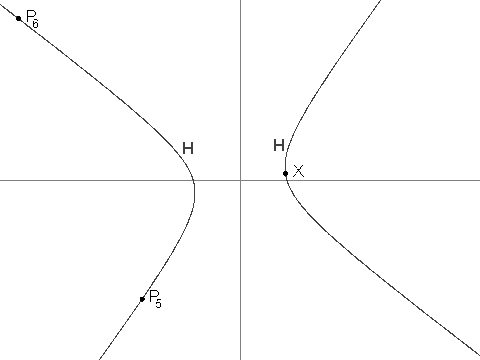
You are given that P3 = (-19/2, -229/24), P4 = (1267/144, -37/12) and P7 = (17194218091/143327232, 274748766781/1719926784).
Find Pn for n = 1114 in the following format:If Pn = (a/b, c/d) where the fractions are in lowest terms and the denominators are positive, then the answer is (a + b + c + d) mod 1 000 000 007.
For n = 7, the answer would have been: 806236837.
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter