Squares under a hyperbola
May 29, 2009
Consider the region constrained by 1 ≤ x and 0 ≤ y ≤ 1/x.
Let S1 be the largest square that can fit under the curve. Let S2 be the largest square that fits in the remaining area, and so on. Let the index of Sn be the pair (left, below) indicating the number of squares to the left of Sn and the number of squares below Sn.
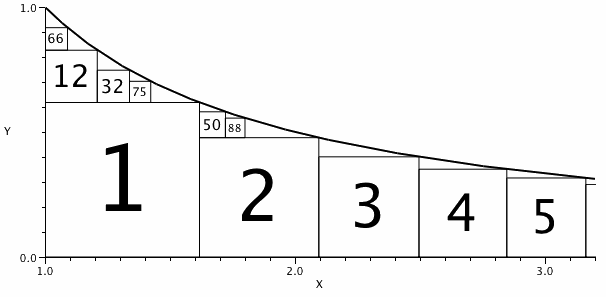
The diagram shows some such squares labelled by number. S2 has one square to its left and none below, so the index of S2 is (1,0). It can be seen that the index of S32 is (1,1) as is the index of S50. 50 is the largest n for which the index of Sn is (1,1).
What is the largest n for which the index of Sn is (3,3)?
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter