Tangents to an ellipse
May 22, 2009
A definition for an ellipse is: Given a circle c with centre M and radius r and a point G such that d(G,M)<r, the locus of the points that are equidistant from c and G form an ellipse.
The construction of the points of the ellipse is shown below.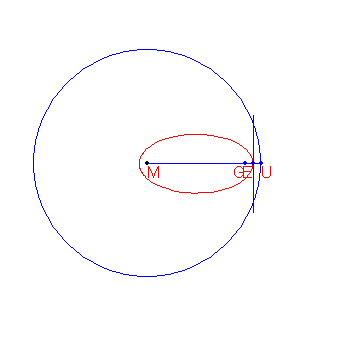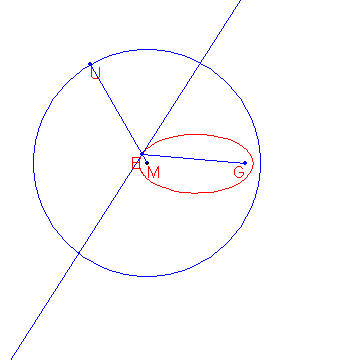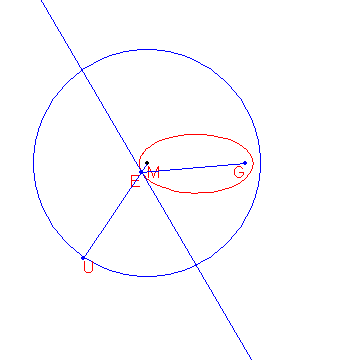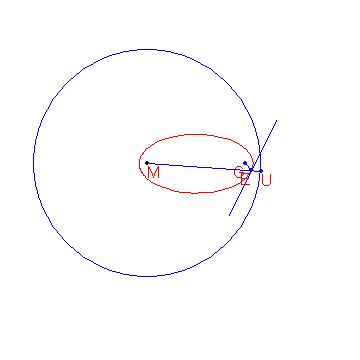
Given are the points M(-2000,1500) and G(8000,1500). Given is also the circle c with centre M and radius 15000. The locus of the points that are equidistant from G and c form an ellipse e. From a point P outside e the two tangents t1 and t2 to the ellipse are drawn. Let the points where t1 and t2 touch the ellipse be R and S.
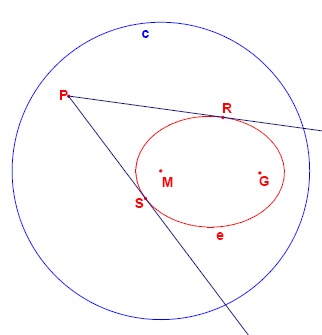
For how many lattice points P is angle RPS greater than 45 degrees?
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter