Three similar triangles
July 03, 2010
Four points with integer coordinates are selected:A(a, 0), B(b, 0), C(0, c) and D(0, d), with 0 < a < b and 0 < c < d. Point P, also with integer coordinates, is chosen on the line AC so that the three triangles ABP, CDP and BDP are all similar.
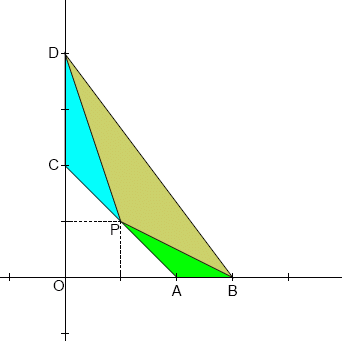
It is easy to prove that the three triangles can be similar, only if a=c.
So, given that a=c, we are looking for triplets (a,b,d) such that at least one point P (with integer coordinates) exists on AC, making the three triangles ABP, CDP and BDP all similar.
For example, if (a,b,d)=(2,3,4), it can be easily verified that point P(1,1) satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point P(1,1) is common for both.
If b+d < 100, there are 92 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000, there are 320471 distinct triplets (a,b,d) such that point P exists.
If b+d < 100 000 000, how many distinct triplets (a,b,d) are there such that point P exists?
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter