Tri-colouring a triangular grid

Consider the following configuration of 64 triangles:

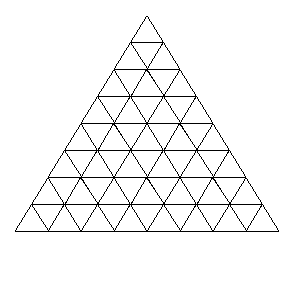
We wish to colour the interior of each triangle with one of three colours: red, green or blue, so that no two neighbouring triangles have the same colour. Such a colouring shall be called valid. Here, two triangles are said to be neighbouring if they share an edge. Note: if they only share a vertex, then they are not neighbours.

For example, here is a valid colouring of the above grid:

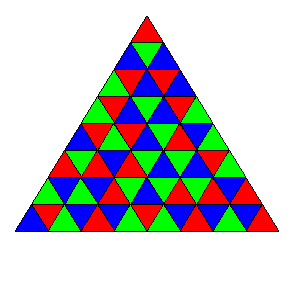
A colouring C' which is obtained from a colouring C by rotation or reflection is considered distinct from C unless the two are identical.

How many distinct valid colourings are there for the above configuration?

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter