Triangle Centres

Consider all the triangles having:

• All their vertices on lattice points.
• Circumcentre at the origin O.
• Orthocentre at the point H(5, 0).

There are nine such triangles having a perimeter ≤ 50. Listed and shown in ascending order of their perimeter, they are:

A(-4, 3), B(5, 0), C(4, -3) A(4, 3), B(5, 0), C(-4, -3) A(-3, 4), B(5, 0), C(3, -4) A(3, 4), B(5, 0), C(-3, -4) A(0, 5), B(5, 0), C(0, -5) A(1, 8), B(8, -1), C(-4, -7) A(8, 1), B(1, -8), C(-4, 7) A(2, 9), B(9, -2), C(-6, -7) A(9, 2), B(2, -9), C(-6, 7)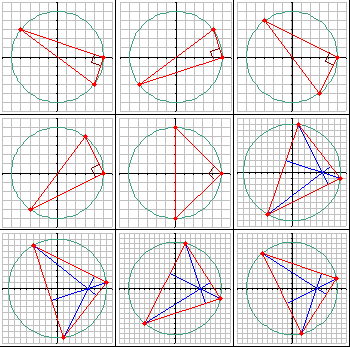

The sum of their perimeters, rounded to four decimal places, is 291.0089.

Find all such triangles with a perimeter ≤ 10⁵. Enter as your answer the sum of their perimeters rounded to four decimal places.

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter