Triangle inscribed in ellipse

The triangle ΔABC is inscribed in an ellipse with equation $\frac {x^2} {a^2} + \frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.

Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\left( \frac a 2, \frac {\sqrt 3} 2 b\right)$.

For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.

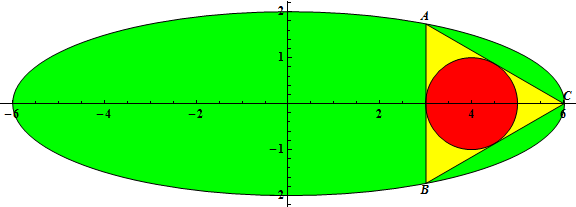
Let $G(n) = \sum_{a=3}^n \sum_{b=1}^{\lfloor \frac {a - 1} 2 \rfloor} r(a, b)$

You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits).

Find G(10¹¹).

Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent.

For G(10) the answer would have been 2.059722222e1.

Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter