Tricoloured Coin Fountains
June 06, 2015
An arrangement of coins in one or more rows with the bottom row being a block without gaps and every coin in a higher row touching exactly two coins in the row below is called a fountain of coins. Let f(n) be the number of possible fountains with n coins. For 4 coins there are three possible arrangements:

Therefore f(4) = 3 while f(10) = 78.
Let T(n) be the number of all possible colourings with three colours for all f(n) different fountains with n coins, given the condition that no two touching coins have the same colour. Below you see the possible colourings for one of the three valid fountains for 4 coins:
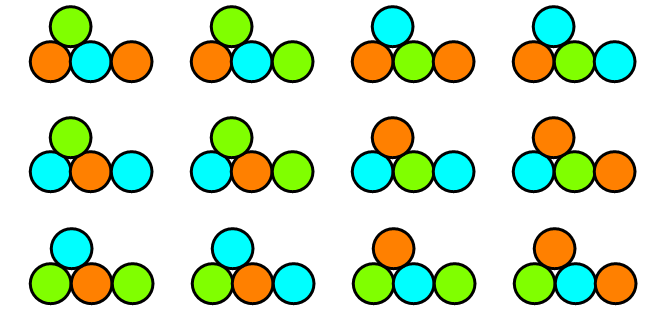
You are given that T(4) = 48 and T(10) = 17760.
Find the last 9 digits of T(20000).
Written by gamwe6 who lives and works in San Francisco building useful things. You should follow him on Twitter